GoMerkle: Learning Go by Implementing Merkle-trees
I have programmed in Python for a few years now and since most of my projects are focused on prototyping and tooling, I haven’t really needed to think about runtime performance or memory footprint. Concepts of strict typing and memory allocation and access have started to feel distant. I figured, might as well give Go a shot, since it checks those skill boxes while still being relatively high level and general purpose. As a starter project, I decided to learn Go by implementing my personal favourite data structure and one that some of my prior research work is based on - merkle trees. The source code: {anishsujanani/gomerkle}.
A Summary of Merkle Trees and the problem they solve
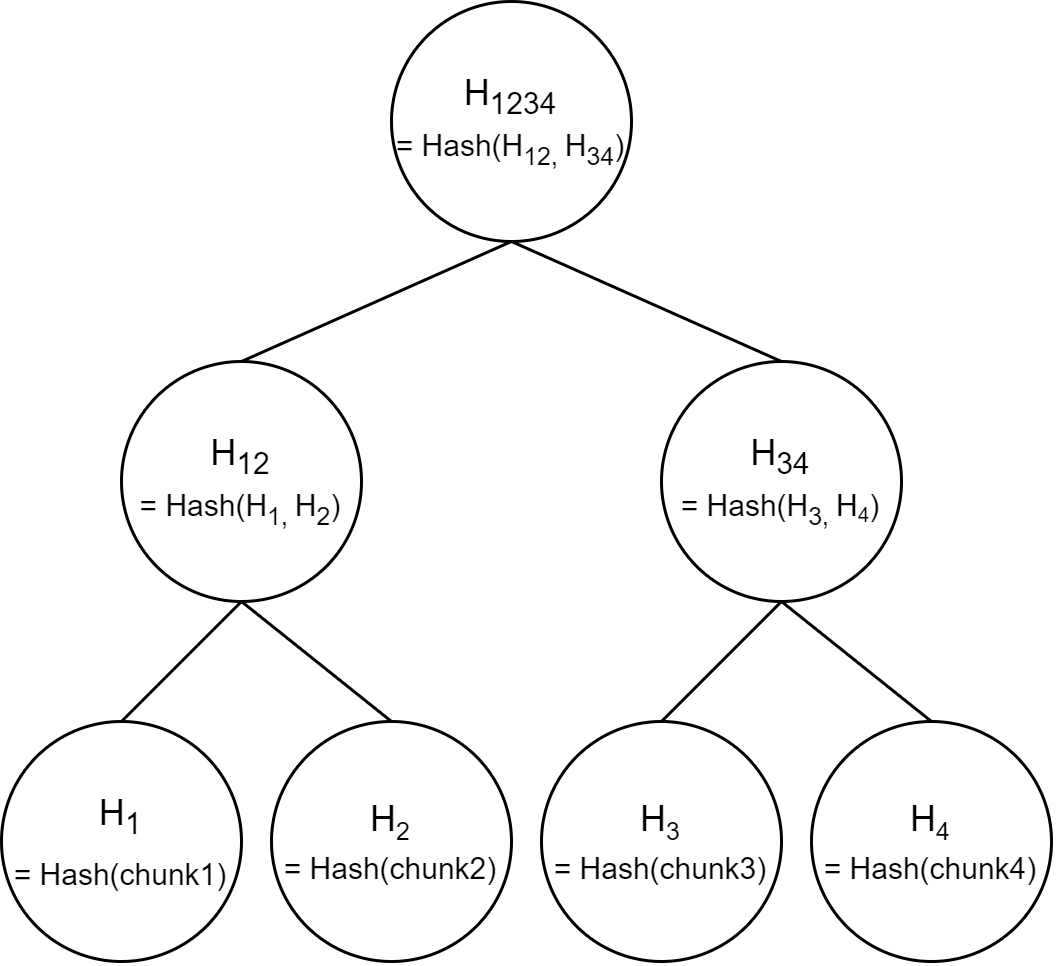
Among others, these data structures play a huge role in integrity verification. Traditional hashing algorithms are able to signify that certain content has been changed from a point of known-good state, however, do not indicate the extent or location of the change. This is the exact problem a merkle tree solves. While they may be n-ary trees, they are typically implemented as balanced binary trees.
Content is split up into chunks, and then hashed. Nodes containing these hashes form the leaves of the tree. Pairs of nodes are iterated over, their values are appended together, and hashed, i.e. a hash of appended hashes. This process is repeated until a root node is formed. Known-good content is put through this process, and the resulting tree is stored.
When trying to verify integrity, if the root-node of the suspect content does not match the known-good root, we know that the content has changed. If the known-good root’s left-child’s value matches the suspect-content root’s left child’s value, we know that that entire subtree maintains integrity, and therefore we no longer need to traverse it. We repeat this search process only on the root’s right child, until:
- We hit a single leaf node, implying that only one chunk has been corrupted
- We hit a parent node whose left and right child are corrupt, implying that all the leaf nodes within that subtree have lost integrity
This O(log n) complexity in pointing out exact points of corruption is the reason merkle trees are so popular and have found literal or conceptual application in blockchain and version control protocols. A prior project I worked on involved detection of opcode tampering within ELF executables and an efficient protocol to remotely patch instructions. (Research)
Why I enjoyed writing this in Go?
Strong Typing
In the past, I never fully understood the hype about type semantics. Though Go supports dynamic typing, I made it a point to use static typing as much as possible, and it resulted in clean, elegant and self-explanatory structures and functions, which lends naturally to error handling, input sanitization and edge-case handling.
Precise and Intentional Code
Taking a moment to think about structures, types, function inputs and return types really made me think about the footprint my binary would put down in memory. It naturally put me in the mindset for performance oriented, highly modular code. More than anything else, it inspired a lot of confidence in running and scaling up to larger applications.
Comment-driven Documentation and Auto-formatting
This is a minor detail and is available in plenty of other languages, but the go doc and gofmt support out of the box was nice to have.
In conclusion, Python is fine for one-time automation, but when it comes to reliable, reproducible tooling and PoCs, I intend to write GoLang a lot more in the near future. I will now leave you with the API that GoMerkle exposes.
The API
go doc -all output from the library is as follows:
package gomerkle // import "github.com/anishsujanani/gomerkle"
Package gomerkle provides functions to create Merkle-trees and perform
common operations on the data structures involved. Anish Sujanani, 2022.
TYPES
type MerkleNode struct {
// Has unexported fields.
}
func MerkleTree(Content string, LeafSize int) MerkleNode
MerkleTree creates the Merkle tree and returns the root node of type
'MerkleNode'.
func (m MerkleNode) BreadthFirstSearch() []MerkleNode
BreadthFirstSearch returns a slice of MerkleNode(s) gathered from a
level-wise ordering of the tree starting from the node it is invoked by.
func (m MerkleNode) DepthFirstSearch(order string) []MerkleNode
DepthFirstSearch returns a slice containing MerkleNode(s) gathered from a
depth-first-search on the tree starting from the node it is invoked by.
Ordering is decided based on the input parameter:
(preorder|inorder|postorder).
func (m MerkleNode) EqualTo(t MerkleNode) bool
EqualTo returns the result of node hash equality. Calling this function with
nodes in corresponding positions in two trees will return the equivalence of
those nodes, and therefore those sub-trees (if they are not leaves).
func (m *MerkleNode) GetHash() string
GetHash returns the SHA-256 hash of a MerkleNode's raw-text.
func (m MerkleNode) GetHeight() int
GetHeight returns the height of the Merkle tree.
func (m MerkleNode) GetInconsistentLeaves(t MerkleNode) []MerkleNode
GetInconsistentLeaves returns a list of MerkleNode(s) from the 't' tree that
differ from the 'm' tree. It is advised to first check if the two trees are
the same height. If heights differ, there is no point in calling this
function as the 't' tree has obviously changed.
func (m MerkleNode) GetLeaves() []MerkleNode
GetLeaves returns a list of MerkleNode(s) representing the leaves of the
tree built from the raw content.
func (m MerkleNode) GetLeftChild() *MerkleNode
GetLeftChild returns the left-child of a MerkleNode.
func (m MerkleNode) GetNodeCount() int
GetNodeCount returns the total number of nodes present in the tree. (2^n)-1
func (m MerkleNode) GetRawText() string
GetRawText returns the raw-text of a MerkleNode.
func (m MerkleNode) GetRightChild() *MerkleNode
GetRightChild returns the right-child of a MerkleNode.
func (m MerkleNode) String() string
Custom fmt.Print* function for the type MerkleNode.
Sample Usage
package main
import (
"fmt"
"github.com/anishsujanani/gomerkle"
)
func main() {
root := gomerkle.MerkleTree("abcdefghijk", 2);
fmt.Printf("-> Root node - default Print(): \n%v\n", root)
fmt.Printf("-> Root node - raw text:\n%v\n\n", root.GetRawText())
fmt.Printf("-> Left child of root - default Print(): \n%v\n", root.GetLeftChild())
fmt.Printf("-> Right child of root - raw text: \n%v\n\n", (root.GetRightChild()).GetRawText())
fmt.Printf("-> Tree height: \n%v\n\n", root.GetHeight())
fmt.Printf("-> Node count: \n%v\n\n", root.GetNodeCount())
fmt.Printf("-> Leaves: \n%v\n\n", root.GetLeaves())
fmt.Printf("-> Breadth First Search (level-wise ordering) - default Print(): \n%v\n\n", root.BreadthFirstSearch())
fmt.Printf("-> Depth First Search (preorder) - custom print: \n")
for _, node := range root.DepthFirstSearch("preorder") {
fmt.Printf("%v ", node.GetRawText())
}
fmt.Printf("\n\n-> DepthFirstSearch (inorder) - custom print: \n")
for _, node := range root.DepthFirstSearch("inorder") {
fmt.Printf("%v ", node.GetRawText())
}
fmt.Printf("\n\n-> Depth First Search (postorder) - custom print: \n%v\n", root.DepthFirstSearch("postorder"))
t := gomerkle.MerkleTree("abxdefyhijz", 2)
fmt.Printf("-> Root equality: \n%v\n\n", root.EqualTo(t))
fmt.Printf("-> Nodes in target tree differing from root tree: \n%v\n", root.GetInconsistentLeaves(t))
}
All opinions expressed on this site are purely my own and are not representative of any other entity.